SVG, la syntaxe Path
L'élément path de SVG est l'outil de dessin le plus perfectionné qui soit, mais sa syntaxe ne semble pas aisée. Chris Coyier décortique brillamment ce langage, pas si compliqué finalement.
L'élément <path> de SVG (path est le chemin) est l’outil de dessin le plus perfectionné qui soit. Il peut dessiner absolument n'importe quoi ! Sous le capot, d'après mes infos, tous les autres éléments utilisent path. Cet élément prend un argument unique pour décrire tout ce qu'il dessine : l'attribut d. Ce dernier a sa syntaxe bien à lui, qui peut paraître indéchiffrable : une kyrielle de chiffres et de lettres qui se suivent. Comme pour tout avec les ordinateurs, il y a une explication et, bien que non expert, j'ai pensé que ça pourrait être amusant de s'y plonger.
Voici un exemple de complexité moyenne :
//SVG
<path d="M213.1,6.7c-32.4-14.4-73.7,0-88.1,30.6C110.6,4.9,67.5-9.5,36.9,
6.7C2.8,22.9-13.4,62.4,13.5,110.9,C33.3,145.1,67.5,170.3,125,217c59.3-46.7,
93.5-71.9,111.5-106.1C263.4,64.2,247.2,22.9,213.1,6.7z"/>On pourrait le reformater ainsi, le code serait toujours valide :
<path d="
M 213.1,6.7
c -32.4-14.4-73.7,0-88.1,30.6
C 110.6,4.9,67.5-9.5,36.9,6.7
C 2.8,22.9-13.4,62.4,13.5,110.9
C 33.3,145.1,67.5,170.3,125,217
c 59.3-46.7,93.5-71.9,111.5-106.1
C 263.4,64.2,247.2,22.9,213.1,6.7z"
/>Les lettres sont des commandes. Les nombres sont des valeurs passées à ces commandes. Toutes les virgules sont optionnelles, on pourrait aussi bien avoir des espaces.
Par exemple, la première commande est M. Métaphoriquement, M dit prend ton crayon et déplace le exactement vers le point de coordonnées 231.1, 6.7. On ne dessine rien pour l'instant, on déplace juste le crayon à ces coordonnées. Si d'autres commandes suivent, elles commenceront à cet endroit.
M est juste une des multiples commandes disponibles pour path. Si j'ai bien compté, il y en a 18 en tout.
La plupart viennent par deux, il y a une version en majuscules et une version en minuscules. La version en majuscules est la version absolue, celle en minuscules est la version relative. Continuons avec notre exemple M :
M 100,100signifie prend le crayon et déplace le exactement au point de coordonnées 100,100.m 100,100signifie déplace le crayon de 100 vers le bas et 100 vers la droite, à partir de l'endroit où tu te trouves.
Beaucoup de commandes fonctionnent ainsi. La version en minuscules intègre la position actuelle du "crayon".
Regardons deux commandes absolues :
Suivies par une commande relative :
De même que les commandes M et m, L et l prennent deux nombres représentant des coordonnées absolues ou relatives. Il y a quatre autres commandes qui sont en fait des versions simplifiées des commandes de ligne. Elles dessinent aussi des lignes, mais ne prennent qu'une seule valeur: horizontale ou verticale. Lorsque nous avons utilisé l 25,0 nous aurions pu utiliser h 25 à la place, qui signifie de l'endroit où se trouve le crayon actuellement, dessine vers la droite, de 25. C'est juste plus succinct. Son grand frère H, comme on le devine, signifie dessiner vers la coordonnée horizontale exacte 25. V et v sont les équivalents pour la direction verticale. Vous vous en doutiez, pas vrai ?
Jetez un coup d'oeil à cette démo de Chris Nager, dans laquelle il dessine une croix avec un code incroyablement concis grâce aux coordonnées relatives :
Vous avez remarqué le dernier caractère utilisé par Chris ? Z.
Z (ou z, ça n'a pas d'importance) "ferme" le chemin. Comme toutes les autres commandes, il est optionnel. C'est une manière facile de tracer une ligne droite directement vers le dernier point où le "crayon" a été posé (probablement une commande M ou m), qui vous évite d'avoir à répéter ce premier point et à utiliser une commande pour y parvenir.
Récapitulons les commandes dont nous disposons jusqu'à présent :
| M x,y | Aller vers les coordonnées absolues x,y |
| m x,y | Aller de x vers la droite et de y vers le bas (ou gauche et haut si les valeurs sont négatives) |
| L x,y | Tracer une ligne droite vers le point de coordonnées absolues x,y |
| l x,y | Tracer une ligne droite vers un point situé à x vers la droite et y vers la gauche relativement (ou gauche et droite si les valeurs sont négatives |
| H x | Tracer une ligne horizontale vers la coordonnée x exacte |
| h x | Tracer une ligne horizontale à droite vers le x relatif (ou vers la gauche si la valeur est négative) |
| V y | Tracer une ligne verticale vers la coordonnée y exacte |
| v y | Tracer une ligne verticale en bas vers le y relatif (ou vers le haut si la valeur est négative) |
| Z (ou z) | Tracer une ligne droite pour revenir au début du chemin |
Pour l'instant, nous n'avons eu affaire qu'à des lignes droites. Path est un élément et une syntaxe parfaitement acceptable pour cela, même si l'on pourrait avancer que des éléments comme <polygon> ont une syntaxe encore plus simple, quoiqu'un peu plus limitée (👉🏾 plus d'infos sur les polygones SVG dans les bases SVG de La Cascade_.)
C'est avec les courbes que path montre ses super-pouvoirs ! Si vous voulez rappelez, le premier extrait de code que nous avons vu comportait un tas de commandes C et c. Ce sont les Courbes de Bézier et elles ont besoin de plus d'infos pour faire leur boulot.
La commande C a besoin de trois points. Les deux premiers définissent la localisation des deux poignées, c'est un concept qui vous est sans doute familier si vous utilisez Adobe Illustrator ou Sketch.

Le dernier des trois points est l'endroit où la courbe s'achève. Voici une illustration de la commande C :
La commande c (minuscule) est exactement la même, sauf que les trois points utilisent des valeurs relatives.
La commande S (ou s) est la petite soeur des commandes C en ce sens qu'elle ne nécessite que deux points : elle suppose que son premier point de Bézier est le dernier point de Bezier de la commande S ou C qui précède.
La commande Q est l'une des plus simples car elle ne requiert que deux points. Le point de Bézier requis est un point de contrôle "quadratique" de la courbe, tout se passe comme si le point de départ et d'arrivée partageaient un point unique qui serait l'extrémité de leur poignée respective.
Autant parler de T dans la foulée : c'est la petite soeur de Q, comme S l'est de C. Lorsque T vient après Q, le point de contrôle est supposé être le même que le précédent, donc on n'a besoin de donner que le point final :
La commande A est sans doute la plus compliquée. Ou du moins celle qui requiert le plus de données. On lui donne l'information définissant un ovale (sa largeur et sa hauteur, ou plus exactement la longueur du rayon x et la longueur du rayon y) et sa rotation, ainsi que le point final. Puis un peu plus d'info pour dire quel chemin vous voulez que votre path prenne le long de cet ovale. Extrait de MDN :
Il y a deux ellipses possibles autour desquelles le chemin peut "voyager" et deux chemins possibles sur chaque ellipse, ce qui donne en tout quatre chemins possibles. Le premier argument est relatif à l'arc le plus grand,
large-arc-flag. Il détermine simplement si l'on choisit l'arc qui est plus grand ou plus petit que 180 degrés; au final, ce flag détermine la direction que suivra l'arc autour d'un cercle donné. Le second argument est lesweep-flag, il détermine si l'arc doit commencer à se mouvoir selon un angle positif ou négatif, ce qui revient à choisir lequel des deux cercles on suit.
NdT : Autre explication, tirée de SVG Ground, une bible (en français) pour SVG :
la lettre qui commande le tracé d’un arc elliptique est A (ou a minuscule pour des coordonnées relatives). Les deux premiers paramètres sont respectivement la longueur du rayon x et la longueur du rayon y (ces deux rayons restent perpendiculaires). Le troisième est la rotation (sens direct, inverse des aiguilles d’une montre) en degrés de l’axe x de l’ellipse par rapport à l’axe des ordonnées. Le quatrième paramètre, appelé large-arc-flag, indique si on doit afficher l’arc dont la mesure fait plus de la moitié du périmètre de l’ellipse (dans ce cas, la valeur est 1), ou l’arc dont la mesure fait moins de la moitié du périmètre (valeur : 0). Le cinquième paramètre, appelé sweep-flag, indique quant à lui si l’arc doit être dessiné dans la direction négative des angles (dans lequel cas sa valeur est 0) ou dans la direction positive des angles (valeur : 1). Les deux derniers sont les coordonnées du point d’arrivée, les coordonnées du point de départ étant données par la commande précédant la commande A. La commande d’arc elliptique est à mon sens assez difficile à comprendre, mais une fois assimilée, elle est très simple d’utilisation. Il faut souvent beaucoup de tests avant de comprendre comment elle fonctionne.
Le graphique de Joni Trythall expliquant la commande A dans son article sur les chemins SVG est assez clair :
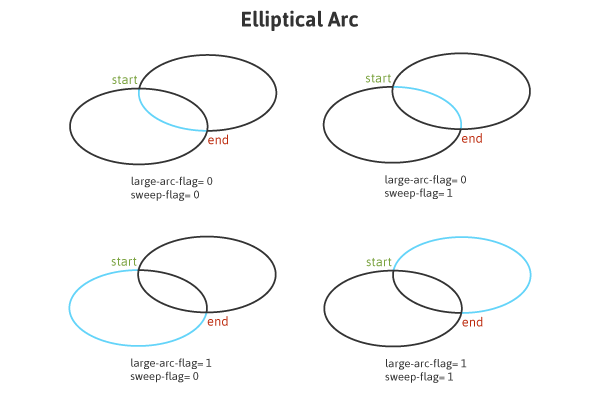
NdT : Exemple (modifié) tiré de l'article de Joni Trythall :
<svg>
<path fill=lightblue
stroke="#333333"
stroke-width="3"
d="M100,20 a100,40 10 1,0 100,10" />
</svg>Le premier et le dernier ensemble de valeurs (M100,20 & 100,10) représentent les coordonnées initiales et finales. Le second ensemble de valeurs (a100,40) définit les deux rayons. Le troisième, la rotation (10). Enfin, les valeurs 1,0 (large-arc-flag & sweep-flag) déterminent la façon dont l'arc est dessiné.
Ce qui donne :
Voici une explication écrite de ces commandes de courbes :
| C cX1,cY1 cX2,cY2 eX,eY | Dessine une courbe de Bezier à partir de deux points de contrôle et se termine à des coordonnées spécifiées |
| c | Idem, avec des valeurs relatives |
| S cX2,cY2 eX,eY | En gros, une commande C qui part du principe que le premier point de contrôle de Bezier est le même que le dernier point de contrôle utilisé dans la commande S or C qui précèdent |
| s | Idem, avec des valeurs relatives |
| Q cX,cY eX,eY | Dessine une courbe de Bezier à partir d'un unique point de contrôle et se termine à des coordonnées spécifiées |
| q | Idem, avec des valeurs relatives |
| T eX,eY | En gros, une commande Q qui part du principe que le premier point de contrôle de Bezier est le même que le dernier point de contrôle utilisé dans la commande Q or T qui précèdent |
| t | Idem, avec des valeurs relatives |
| A rX,rY rotation, arc, sweep, eX,eY | Dessine un arc basé sur la courbe d'un ovale. Définit d'abord la largeur et la hauteur de l'ovale. Puis la rotation de l'ovale. Avec le point final, cela fait deux ovales possibles. L'arc et la courbe ont pour valeur 0 ou 1 et déterminent quel ovale et quel chemin sera pris. |
| a | Idem, avec des valeurs relatives pour eX,eY |
Vous voulez voir des exemples ? OK :
Si vous le regardez avec un navigateur Blink récent et que vous avez une souris, vous verrez quelques animations au survol ! Eh oui, on peut mettre des données de path dans CSS maintenant, par exemple :
//SVG
<svg viewBox="0 0 10 10">
<path d="M2,5 C2,8 8,8 8,5" />
</svg>et :
//CSS
svg:hover path {
transition: d 0.2s;
d: path("M2,5 C2,2 8,2 8,5");
}