Dans l’article précédent, nous avons vu avec surprise à quel point il était difficile de retrouver une équivalence visuelle entre dimensions et alignements. Notre prochain défi — qui lui non plus ne semble pas en être un au départ — est de gérer les graisses différentes, à la fois au niveau d’une lettre et au niveau d’un groupe de lettres.

Imaginons que nous voulions dessiner quelque chose de simple : une police de caractères sans empattement (sans serif) avec une graisse identique dans tous les cas de figure. Nous choisissons les dimensions et nous commençons à construire les formes.

Mais après les deux premières, une base verticale et une barre horizontale, tout s’écroule. L’horizontale semble plus lourde que la verticale, notre beau plan tombe à l’eau. Nous voulions appliquer les mêmes mesures de manière uniforme, et voilà que nous en avons (apparemment) deux. Pourtant, nous venons de les mesurer et nous savons qu’elles sont égales. Ou plutôt “égales”.

Nos yeux ne voient pas toutes les formes de la même façon, par exemple ils voient les formes horizontales plus lourdes qu’elles ne sont. Ce phénomène a fait l’objet de descriptions multiples, depuis la théorie de “l’inférence inconsciente” de la perception visuelle, jusqu’à la sagesse populaire sur les vêtements rayés nous faisant paraître plus minces ou plus grands. Dans ces exemples et dans bien d’autres, nous sommes trompés par les changements d’orientation. Pour contrecarrer cette mauvaise interprétation, nous devons alléger la graisse des horizontales jusqu’à ce qu’elles aient l’air égales aux verticales. En d’autres termes, nous avons besoin de graisses multiples pour donner l’illusion d’une graisse unique.

Dans cette vaste entreprise de traficotage, nous nous retrouvons malgré tout en bonne compagnie. Futura, l’exemple ultime de la stricte géométrie, fait les mêmes concessions sous ses airs de pureté. Nous jurerions que ce O est un cercle parfait dessiné par un compas impartial. Mais si nous basculons la forme d’un quart de tour, nous faisons apparaître la supercherie optique et nous voyons la forme telle qu’elle est : une ellipse à l’intérieur d’un cercle.

(Il m’a fallu du temps pour l’accepter après m’en être aperçu. “Bien sûr que ces formes géométriques sont pures. Elles doivent l’être, n’est-ce pas ? Oui ? Sil vous plaît…” C’était comme d’apprendre que la petite souris n’existe pas.)

Cette relation déséquilibrée des verticales et des horizontales se retrouve dans tous les styles. Les deux designs ci-dessus, bien que d’apparence très différente, fonctionnent selon le même principe de contraste des graisses. L’une est recherchée et subtile, l’autre est bruyante et mélodramatique. Sur les plans culturel, émotionnel et pratique, ces designs de l’Europe moderniste et de l’Amérique victorienne n’ont rien à voir. Mais sur le plan optique, ils sont construits selon le même schéma, avec une simple différence d’intensité. Le contraste ne disparaît jamais complètement.

Ce design nous montre un autre conflit fréquent, cette fois-ci entre les formes droites et incurvées. Si nous nous approchons et que nous mesurons les éléments droits et courbes, nous constatons que ce bel ordonnancement précis est fait de disparités.

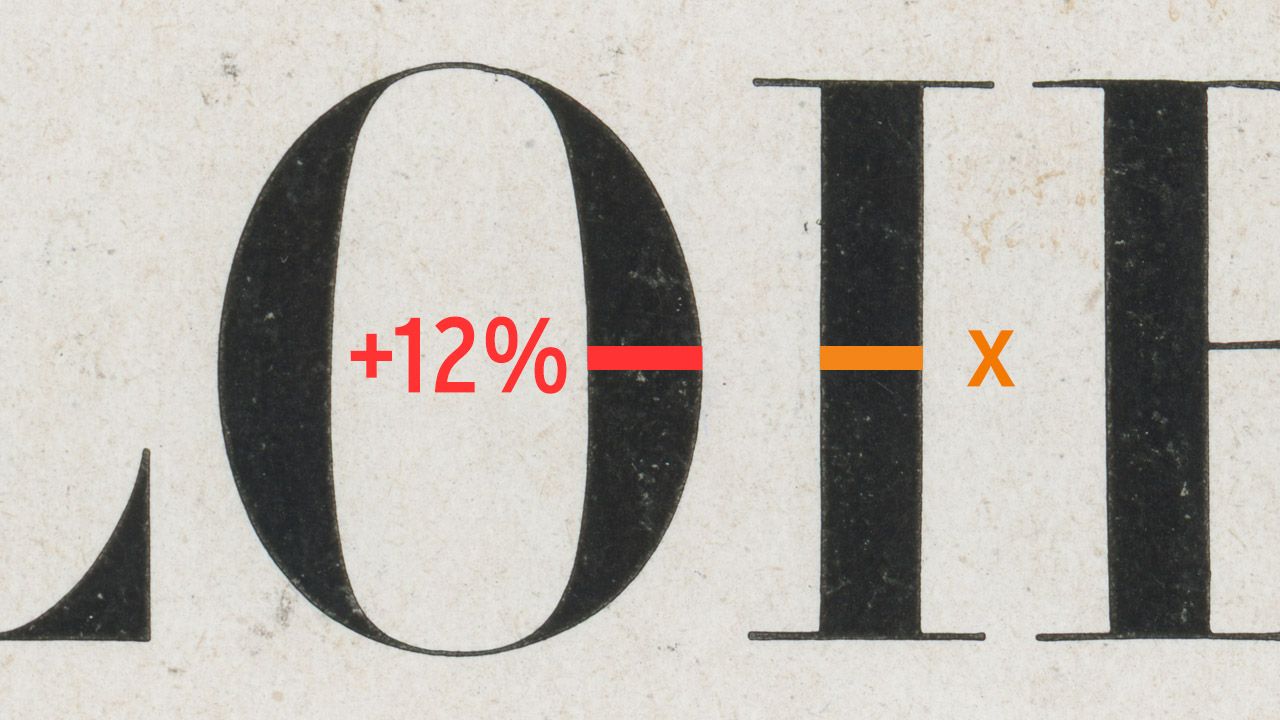
Un poids supplémentaire a été ajouté aux formes incurvées qui, à leur maximum, sont 12% plus larges que les verticales. Le problème sous-jacent et sa solution correspondent en grande partie à ce que nous avons vu avec les alignements dans l’article précédent.

Une courbe atteint son épaisseur maximale en un seul point à son centre, alors que les autres parties deviennent progressivement plus légères. La colonne droite quant à elle conserve son épaisseur du sommet jusqu’en bas. La seule façon de leur donner un air égal est de donner plus d’épaisseur aux parties incurvées, de la même façon que nous avions dû les étendre vers le haut et vers le bas.

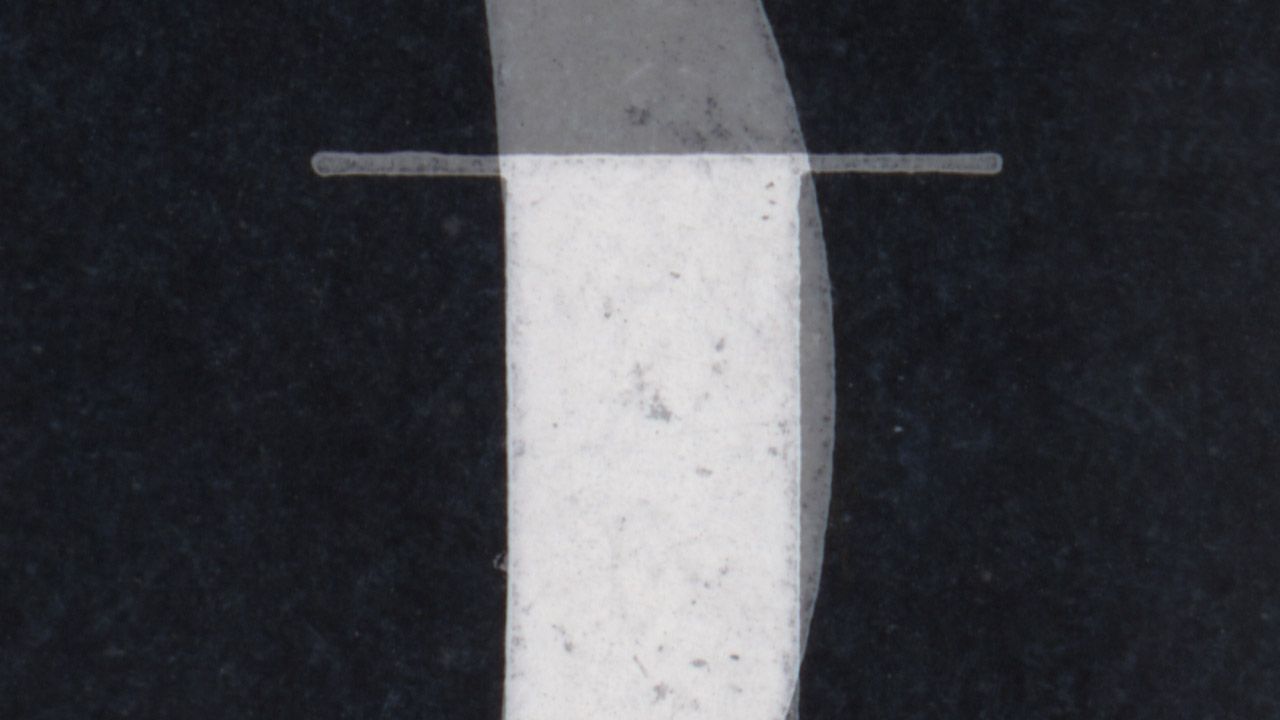
Si le travail est bien fait, cette différence sera à peine perceptible. Mais si nous superposons les formes, nous pouvons voir à quel point les fonderies trichent avec l’épaisseur des courbes pour leur donner un air correct.

Nous avons vu précédemment que le “dépassement” (overshoot) est fonction du type de courbe : moindre lorsque la courbe tend vers une forme carrée, maximum lorsqu’elle est plus ronde. Ici, nous avons les mêmes conditions et conséquences, avec cette masse supplémentaire nécessitée par le contraste. Ci-dessus, Candida offre certains contrastes remarquables, bien que moins accentués que dans le style néoclassique que nous venons de voir. Au-dessous, Memphis est une égyptienne (_slab serif_) sans contraste apparent.

À mesure que le contraste diminue, l’écart entre épaisseur maximum et minimum se réduit. Lorsque l’épaisseur du trait varie moins, on a moins besoin d’ajouter une masse supplémentaire.

Si nous reprenons nos mesures, nous nous apercevons qu’un contraste moindre nécessite moins de masse supplémentaire. Candida augmente l’épaisseur de son trait de 9% alors que le faible contraste de Memphis ne nécessite que 1%. Par conséquent, si vous avez noté comme règle 12% à partir de l’exemple précédent, vous pouvez le rayer : il n’y a pas de formule universelle, mais uniquement des situations particulières, parfois au niveau d’une seule lettre, parfois au niveau de l’alphabet ou de la famille tout entière.

Au bout du compte, tout revient à ajouter du noir lorsqu’il y a trop de blanc. Mais ailleurs dans notre design — voire dans la même lettre — nous pouvons avoir le problème inverse, où nous devons supprimer du noir parce qu’il n’y a pas assez de blanc.

Pour prendre à nouveau un exemple simplifié, nous avons ici un ensemble de lignes séparées par un espace constant. Admettons que nous voulions les rapprocher — les condenser si vous voulez.

Si nous modifions l’intervalle blanc, sans rien changer d’autre, cela aboutit à un résultat inattendu (du moins si nous pensions conserver la même luminosité). La proportion de noir et de blanc a changé, et c’est de là que nous percevons la lumière, pas des dimensions de tel ou tel élément. Alors, si moins de blanc donne l’impression de plus de noir, pouvons-nous redimensionner les éléments de façon à ce que le ratio noir-blanc reste intact ?

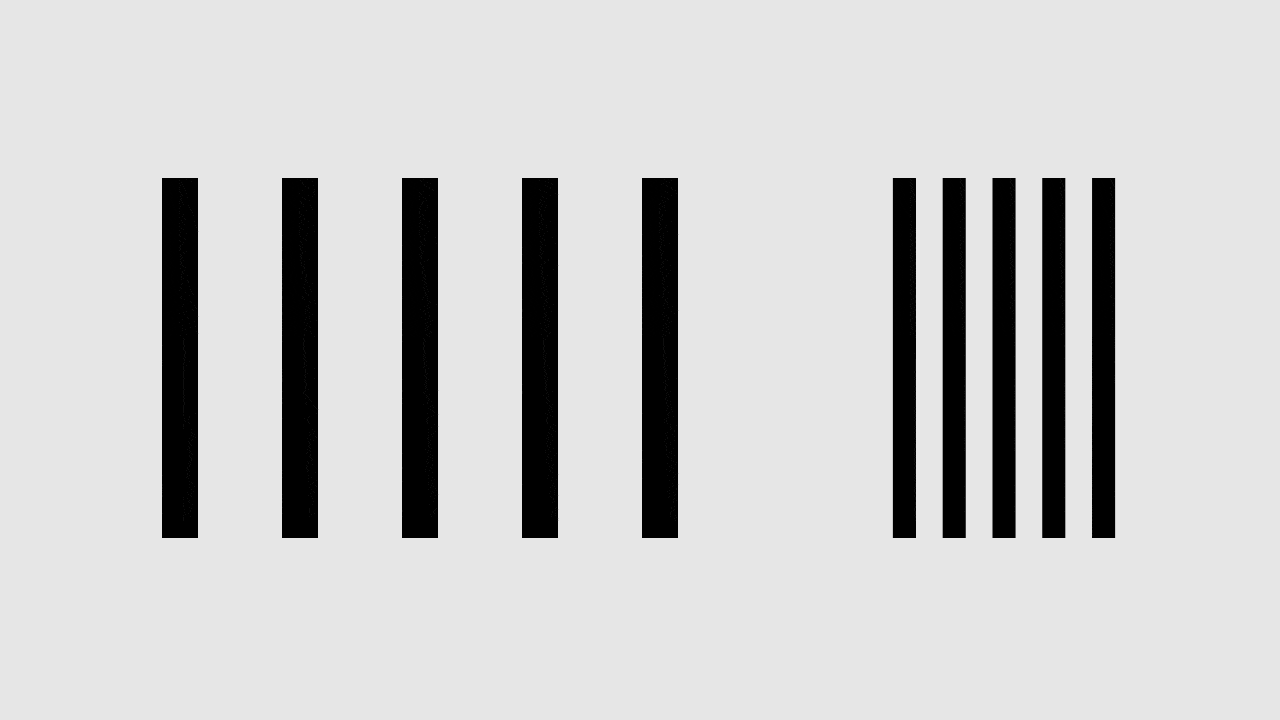
Hélas, ça ne marche pas. Tout devient trop léger à droite car nous voyons que l’épaisseur des traits ne correspond pas. Au passage, c’est la raison pour laquelle les fausses petites capitales (small caps) ont l’air maigrichonnes. En redimensionnant les lettres capitales on crée des caractères dont le poids est différent comme dans l’exemple précédent.

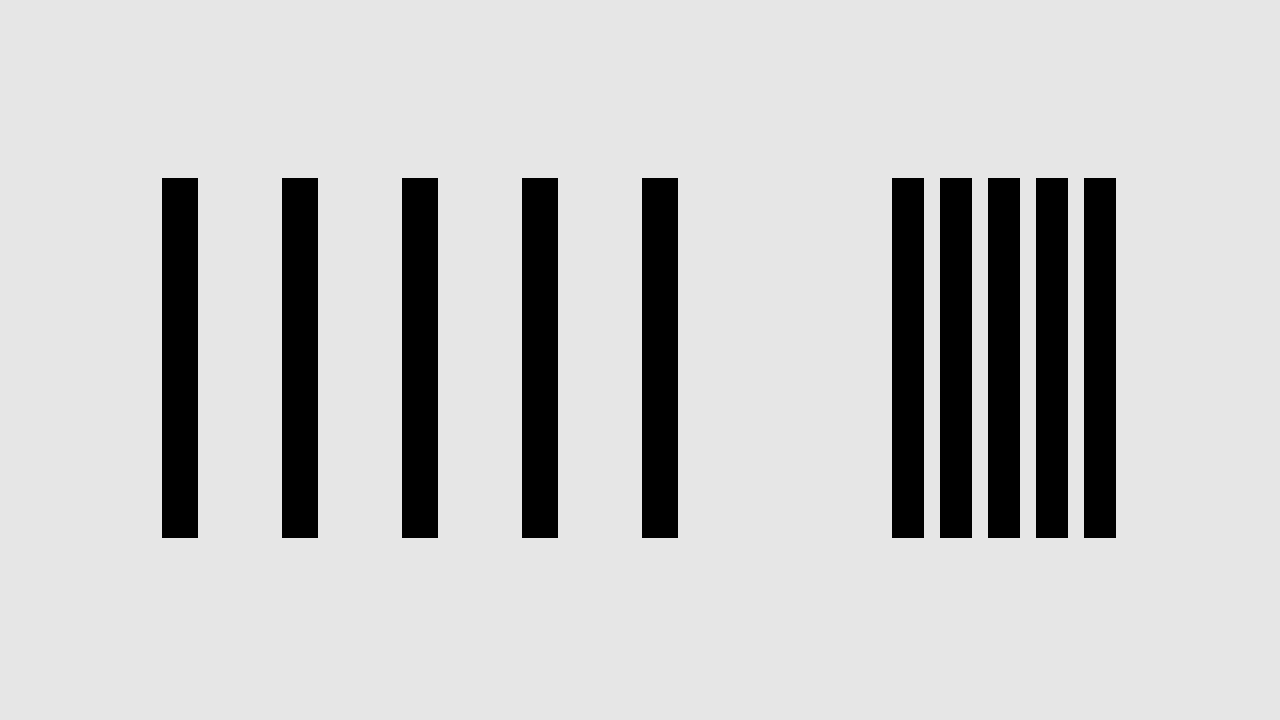
Donc, quand nous rééquilibrons les choses en mettant une épaisseur de trait et un espacement qui ont l’air corrects, nous créons une relation qui n’est ni arithmétique ni géométrique, mais quelque part entre les deux. Nos yeux sont exigeants, ils acceptent rarement la solution la plus simple.

Ce problème de ratio noir/blanc apparaît à l’intérieur même des lettres. Lorsque les bordures des traits sont conservées mécaniquement parallèles, nous constatons un empilement de graisses à l’endroit où ils se croisent. Le centre du x semble vouloir se gonfler, tandis que le v a l’air d’être en caractère gras au sommet et extra-gras en bas. Nous pouvons corriger tout cela en amincissant les traits à l’approche de leur intersection, ce qui stabilise partiellement le ratio de noir et de blanc.

Les graisses s’accumulent en fonction de l’angle de l’intersection, le problème devenant plus aigu à mesure que l’angle est plus pointu. Voilà pourquoi les designers de polices de caractères respirent profondément avant de se lancer dans une version Compressed Extra Bold d’une police, et c’est aussi la raison pour laquelle ils lancent des jurons au W majuscule (ça c’est moi !).

Pour en avoir une vue différente (et en couleur), j’ai demandé à ma collègue Nina Stössinger d’écrire un petit programme en Python qui repère ces changements de graisses et modifie la couleur en fonction. Cela illumine littéralement l’amincissement des traits, dont on voit qu’il s’accélère aux intersections. Il fait également apparaître que la partie gauche du v est plus lourde que la partie droite — mais c’est tout une autre histoire que je vous raconterai la prochaine fois.